Il quesito di gennaio 2013 (533), intitolato  «Il venerabilissimo Eudoxyz» è così formulato:

Disegnare un pentagono concentrico con un cerchio di raggio dato in modo che i cinque rettangoli uguali aventi come uno dei lati il lato del pentagono e per l’altro lato il segmento perpendicolare al precedente e delimitato dalla circonferenza data, abbiano area massima.

La soluzione che ho proposto è la seguente:

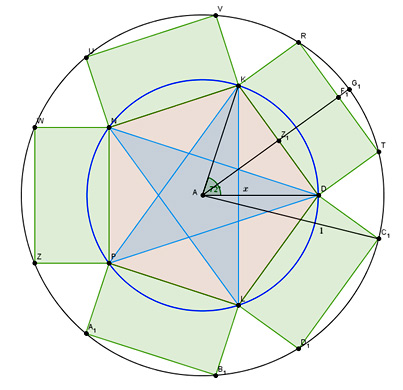
Il pentagono che produrrà i cinque rettangoli di area massima è quello che ha come lato quello che avrebbe il decagono (regolare) inscritto in quella stessa circonferenza. Vale a dire che il suo lato sarà uguale alla sezione aurea del raggio del cerchio.

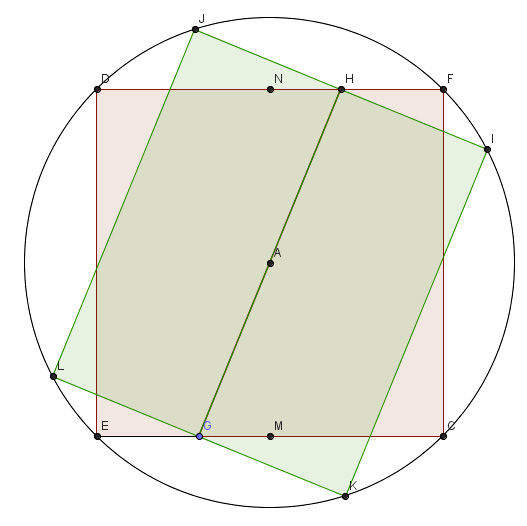
Ecco il disegno che rappresenta tutte le figure geometriche coinvolte:

La dimostrazione completa è disponibile in questo pdf (cliccare sull’immagine che segue):

Da questo link si apre una nuova pagina html in cui è attiva l’applet di GeoGebra per vedere cosa succede quando si modifica la dimensione del pentagono interno.

Da quest’altro invece si apre una pagina simile alla precedente ma che contiene anche le misure dei segmenti e delle superfici. Inoltre, da un’apposita casella, si può inserire il valore del raggio del cerchio in cui è inscritto il pentagono richiesto per vedere il risultato.

Infine ecco le animazioni delle generalizzazioni: la prima per il triangolo/esagono (non interattiva) e la seconda per il caso del quadrato/ottagono (interattiva).

Questo è il link per la cartella zippata che contiene quattro file ggb per Geogebra che generano le figure che ho mostrato.

Ecco il link alla pagina del sito di Le Scienze che contiene il problema, le soluzioni e il blog:

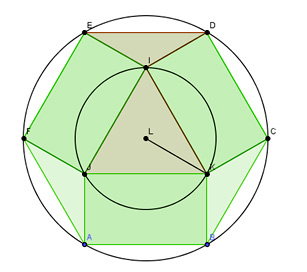
GENERALIZZAZIONE DEL PROBLEMA

La proprietà sopra enunciata per il pentagono può essere generalizzata per tutti i poligoni nel seguente modo:

 l’area massima dei rettangoli costruiti sui lati  di un poligono regolare con n lati concentrico con un cerchio di raggio r, si ha quando il lato del poligono ha lunghezza pari a quello di 2n lati inscritto nel cerchio dato.

 Come conseguenza, ad esempio, il triangolo equilatero concentrico con il cerchio di raggio 1 per il quale i rettangoli costruiti sui lati hanno area massima, è il triangolo avente come lato quello dell’esagono regolare inscritto nel cerchio che, com’è noto, ha lunghezza 1.

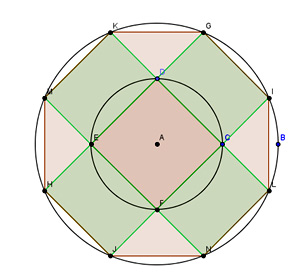
La stessa cosa accade con il quadrato, per il quale i rettangoli hanno l’area massima quando il lato su cui sono costruiti hanno lunghezza pari a quella dell’ottagono regolare  inscritto nella circonferenza. Se questa ha raggio 1 il valore del lato è 0,765366:

GENERALIZZAZIONE FINALE.

A questo punto, faccio la considerazione finale. Il lettore mi segua pazientemente.

Applichiamo la proprietà precedente — cioè la generalizzazione — in senso inverso. Si potrebbe enunciare così:

Il lato di un poligono regolare inscritto in una circonferenza di numero pari di lati (poniamo 2n) è uguale alla lunghezza dei lati di un poligono regolare di metà numero di lati e concentrico con il precedente, per il quale sia massima l’area dei rettangoli costruiti sui suoi n lati e delimitati dalla circonferenza.

Fin qui niente di strano. L’esagono produrrebbe un triangolo per il quale abbiamo già visto valere la proprietà, il dodecagono produrrebbe un esagono più piccolo e… e così via.
Proviamo però a considerare il quadrato come poligono di partenza, cioè quello con numero 2n di lati. Dal quadrato dovremmo ottenere un poligono con metà numero di lati e per il quale dovrebbe valere la stessa proprietà. Questo “poligono” avrebbe però… due lati!
Certo, lo sappiamo, è un poligono che non può esistere. Non c’è la fatidica spezzata che dovrebbe racchiudere una porzione di piano, ecc… .

Ma ammettiamo — per amore di ragionamento, si capisce — di concedere lo status di poligono a questo strano oggetto.

Potremmo anche farcene una ragione, immaginando di rimpicciolire sempre più il terzo lato di un triangolo (equilatero) fino a farlo sparire completamente, portando i vertici a diventare due, come quando si chiude un compasso. Non si può essere obbligati a dire che si ottiene un singolo segmento, potendo benissimo essere visto come due segmenti sovrapposti che, pur se costretti a occupare la stessa “sottile” posizione, sono pur sempre due segmenti distinti.
Uno va da A a B e l’altro va da B ad A. In fondo è lo stesso concetto dei due punti coincidenti che si adopera per definire la tangenza di retta e curva.

Ma torniamo al nostro aspirante poligono. Se fosse davvero tale dovrebbe condividere con gli altri la proprietà generalizzata che ho enunciato.
Per verificarlo usiamo lo stesso procedimento che si usa per passare dall’esagono (ad esempio) al triangolo. Cioè, prendendo il poligono con 2n lati – nel nostro caso il quadrato inscritto nella circonferenza – tracciamo le perpendicolari ai lati che sappiamo già essere i lati dei rettangoli e dei quali ci manca solo l’altezza.
I punti che saranno gli estremi dei lati del “poligono” piccolo li otteniamo dall’intersezione delle perpendicolari dei lati non consecutivi del quadrato (come d’altronde si deve fare per l’esagono).
Ora però accade che i lati non consecutivi del quadrato sono quelli che si trovano l’uno di fronte all’altro e le perpendicolari sono  coincidenti. Questo significa che il punto di intersezione non è determinato potendo essere uno qualunque, anzi tutti, i punti appartenenti agli altri due lati con il vincolo però della simmetria rispetto al centro. Prendiamo allora uno qualunque dei punti e, con la simmetria di cui sopra, anche il secondo.
Si ottiene la figura che segue in cui G e H sono i punti di cui si parla. I due rettangoli verdi, che al solito sono quelli richiesti dal problema, hanno area massima quando G e H corrispondono rispettivamente a M e N. In tale situazione la somma delle aree dei rettangoli uguagliano quella dell’intero quadrato originario e i “lati” del poligono sono uguali al lato del quadrato. Ecco la figura che si ottiene (da questo link si va all’animazione con GeoGebra):

Il “poligono” con due lati, avrà superato il test per essere ammesso nel novero di questa nobile famiglia che di norma accetta solo membri con almeno tre lati?
Per essere chiuso in effetti il “poligono” è chiuso; la porzione di piano delimitata è definita, anche se è zero, che è pur sempre un signor numero. Inoltre, secondo la definizione, deve essere definito convesso poiché tutti i punti del segmento che congiunge due qualsiasi suoi punti appartengono al “poligono”.

Ai posteri l’ardua sentenza!

 Post Post Scriptum.

Con il quadrato, poligono con 4 lati, si chiude la possibilità di tentare a ritroso la scoperta di nuovi poligoni. Al triangolo manca la condizione necessaria e cioè quella di avere un numero pari di lati… altrimenti…

Post Post Post Scriptum

Ma allora perché non provare anche con il “poligono” a due lati per vedere se riesce a generarne uno con un lato. In fondo si parte da un numero pari di lati e quindi la cosa sarebbe fattibile.

Io però declino l’incarico!